密码技术初识

版权属于出版社和作者所有。除非另有声明，没有书面许可任何人不得转载或使用整体或任何部分的内容。此文章只作为个人读书笔记使用。

1. 密码概述 1.1 通信过程中会有哪些主要角色? 1.2 信息安全中所面临的威胁与应对这些威胁的密码技术有什么？ 1.3 隐写术 1.4一些信息安全常识
2. 历史上的密码

密码概述

通信过程中会有哪些主要角色?

名称	说明
Alice	一般角色
Bob	一般角色
Eve	窃听者，可窃听通信内容
Mallory	主动攻击者，可妨碍通信、伪造消息
Trent	可信的第三方
Victor	验证者

信息安全中所面临的威胁与应对这些威胁的密码技术有什么？

其他知识

我们先准备一段话，

很容易看懂就可以，

喜闻乐见的当然更好。

欢迎你尝试将一句话嵌入在这段话中，

你会发现这是一种隐写术。

上面的消息影藏方式是隐写术，隐藏消息本身（而密码技术隐藏的是消息内容）。

数字水印技术就利用了隐写术（一种把著作权拥有者及购买者的信息嵌入文件的技术）。

一些信息安全常识：

• 不要使用保密的密码算法。（开发高强度密码算法极其困难，自己的密码算法一旦暴露很容易被破解）
• 使用低强度的密码比不使用任何密码更危险。（麻痹大意）
• 任何密码总有一天都会被破解。（一次性密码本除外）
• 密码是指信息安全的一部分。（最脆弱的环节往往是人类自己----社会工程学）

历史上的密码

凯撒密码（字母代换）

将一个字母表向指定方向平移N位，解密反之，N为密钥 。

密钥只可能是0-25共26个，用1-25每个数作为密钥尝试解密，很容易发现明文，从而得出密钥是几。（暴力破解）

简单替换密码

两个字母表中字母之间随机一一对应， 密钥是替换表。

密钥空间是 26！= 2^88。所以考虑使用（频率破解）。

对称密码

• DES（Data Encryption Standard）（不再推荐）
• AES（Advanced Encryption Standard） （应该使用）

最新对称密码标准----AES

AES 目前采用的是Rijndael 算法，Rijndael 的分组长度可以是以32bit为单位在128到256范围内选择。目前AES 规定分组长度只能有128,192,256三种。

AES 一轮的步骤：

• 加密：SubBytes —> ShiftRows —> MixColumns —> AddRoundKey
• 解密：AddRoundKey —> InvMixColumns —> InvShiftRows —> InvSubBytes

其中步骤的含义为：

1. SubBytes： 每个字节的值（0-255的任意值）为索引，从一张拥有256个值的替换表（S-Box）中查找对应的值处理。将一个1字节的值替换成另一个1字节的值。
2. ShiftRows：将4个字节为单位的行（Row）按照一定的规则左平移。
3. MixColumns：将一个4字节的值进行比特运算，变成另一个4字节的值。
4. AddRoundKey ：将MixColumns的输出与轮密钥XOR。

对称密码的分组模式

模式：AES 和 DES 都是分组密码，分组密码一次只能加密固定长度的明文。如果需要加密任意长度的明文，就需要对分组密码进行迭代，迭代的方法就称为"模式"。

电子密码本模式（ECB）

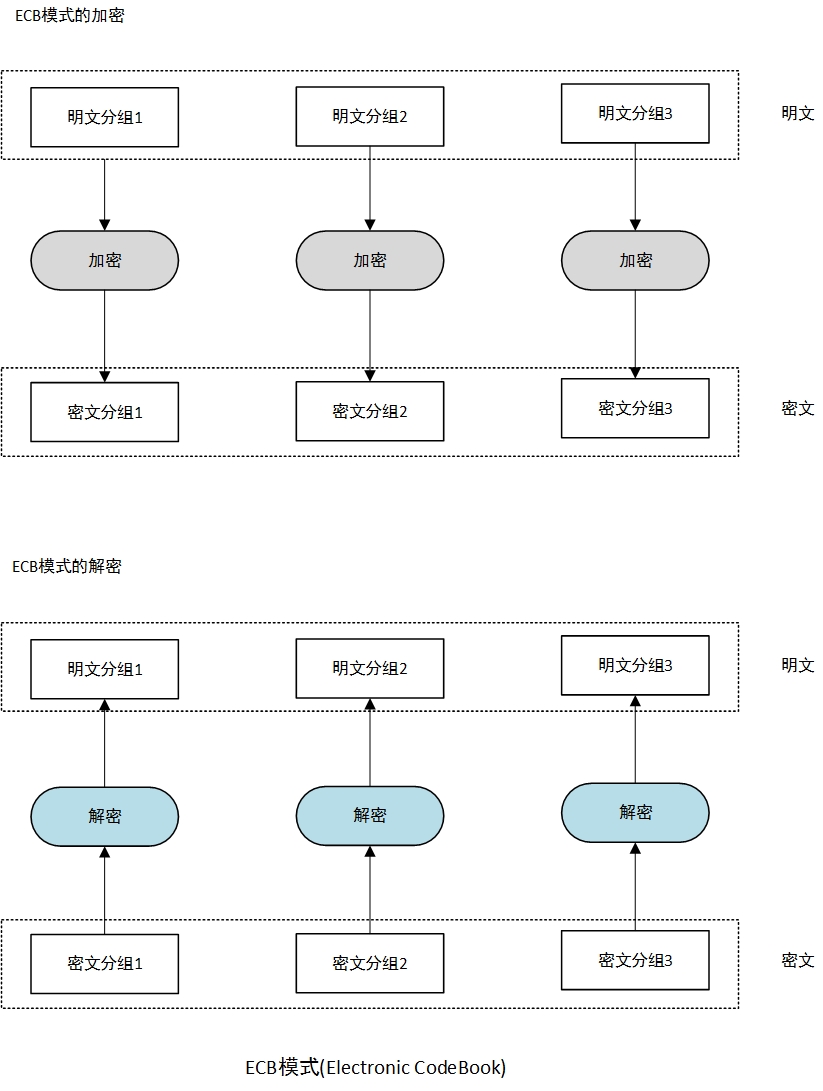
此方法过于简单，不建议使用。

密文分组链接模式（CBC）

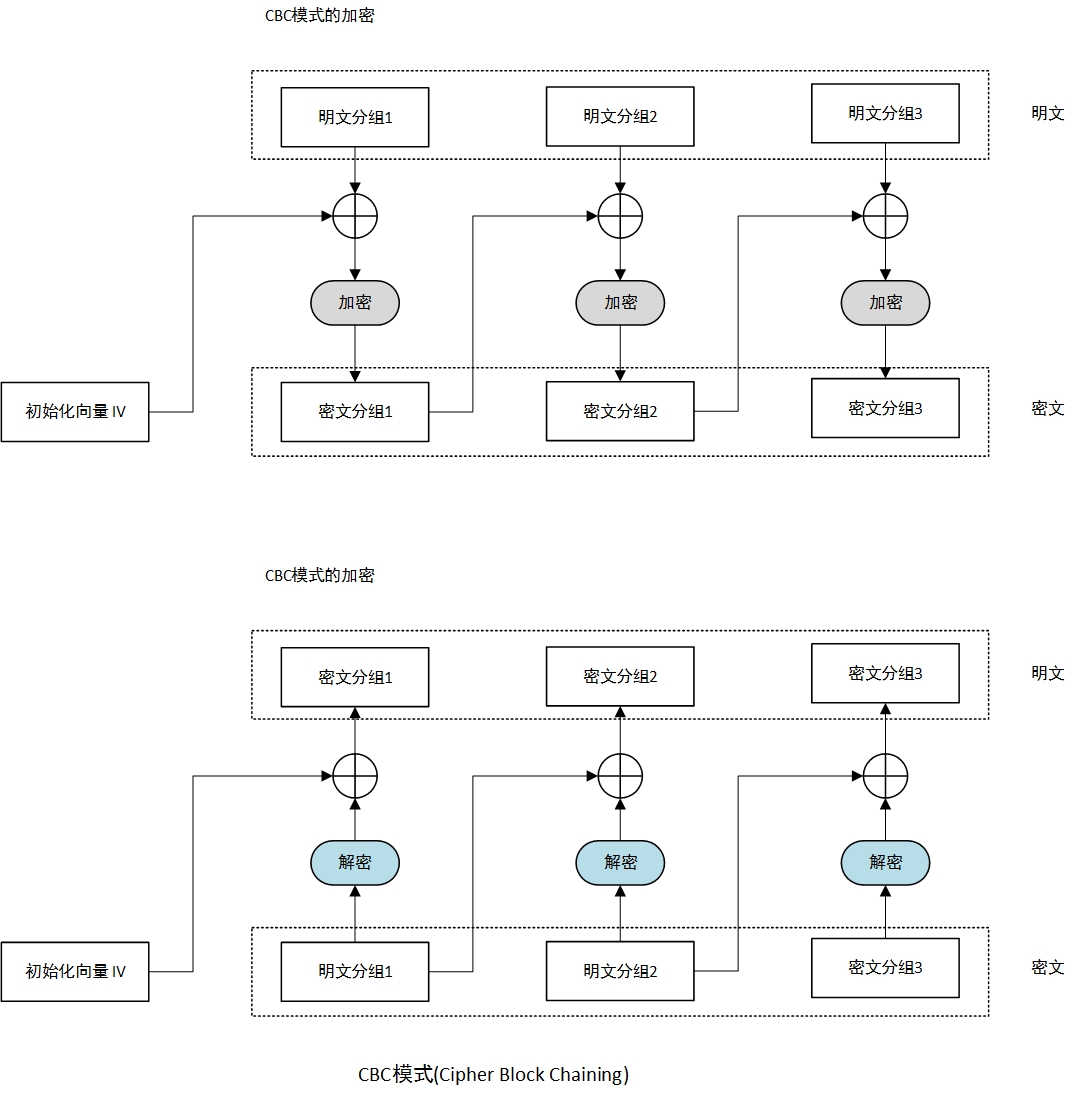
• 初始化向量是一个随机产生的比特序列，IV的生成算法要足够优秀。
• 初始化向量与明文分组XOR后加密生成第一个密文分组，之后的迭代都是将当前生成的密文分组与下一个明文分组XOR后加密生成下一个密文分组。

密文反馈模式 （CFB）

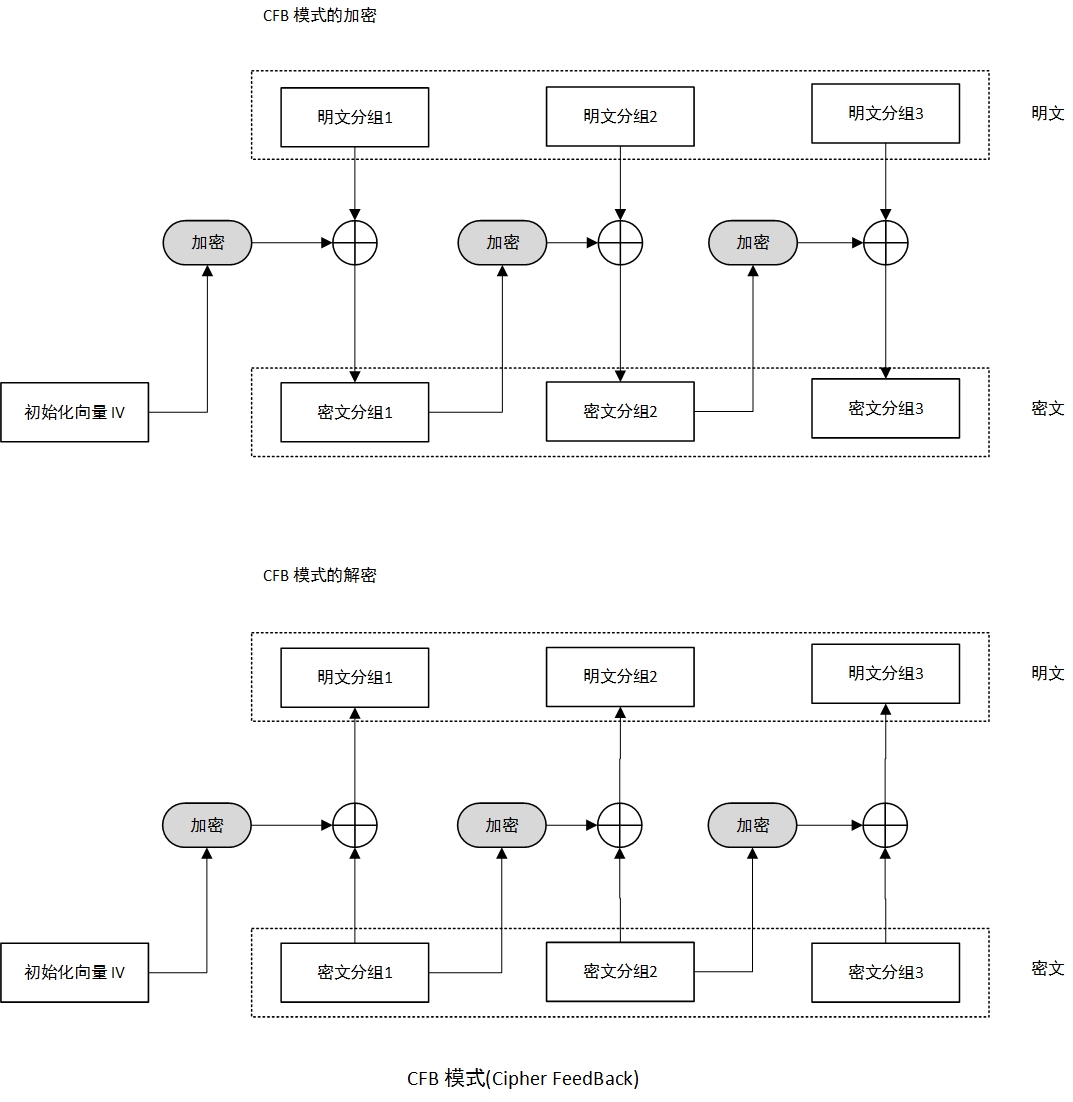
• 初始化向量加密后与第一个明文分组XOR生成第一个密文分组，之后都是当前的密文分组加密后与下一明文分组XOR生成下一个密文分组。
• 密文反馈模式CFB 与 密文分组连接模式CBC的区别在于，密文反馈模式是先加密再XOR，密文分组连接模式是先XOR 再加密。

输出反馈模式（OFB）

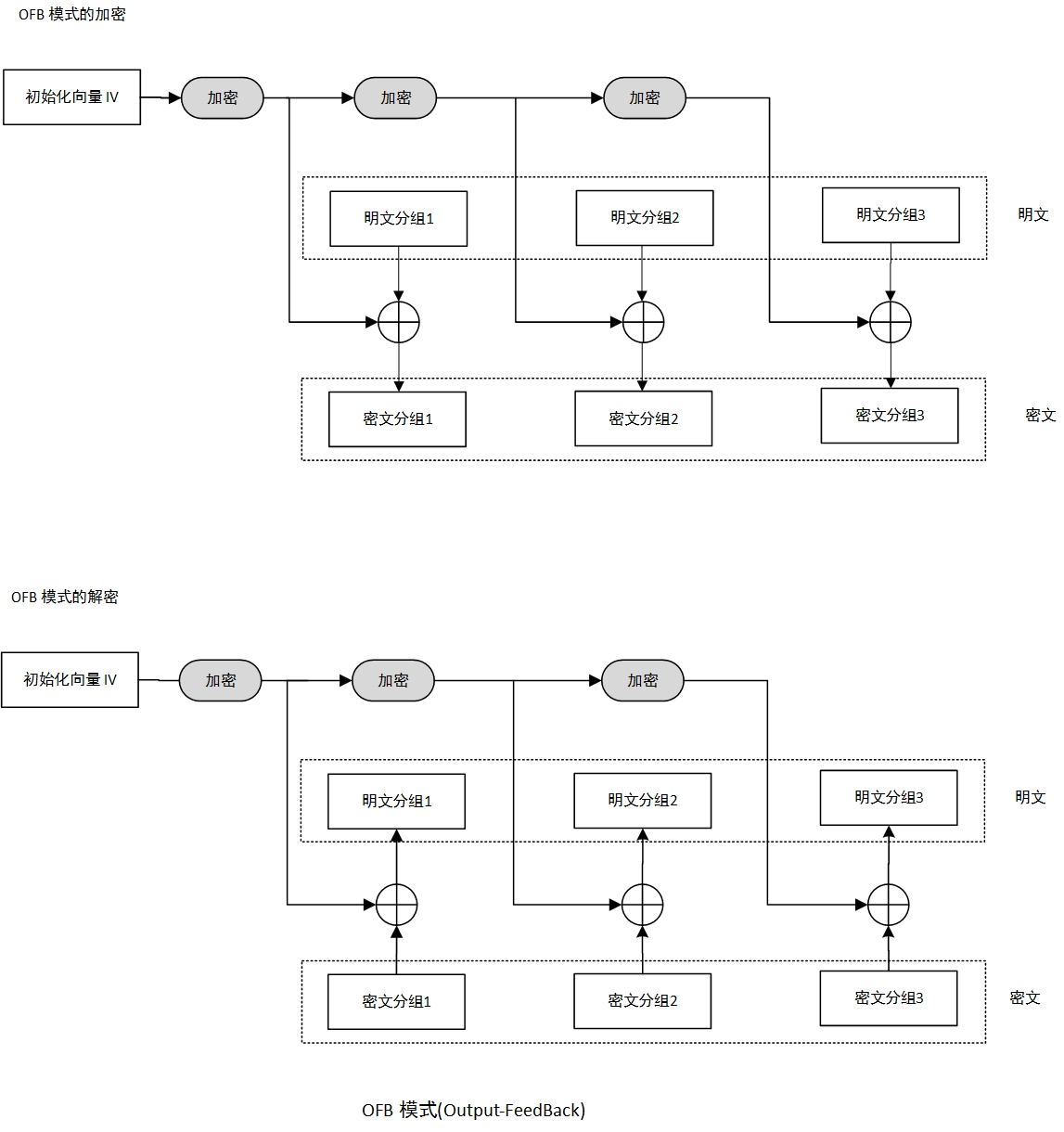
• IV 加密的输出与第一个明文分组XOR 得到第一个密文分组，将加密后的IV 再加密与下一个明文分组XOR得到下一个密文分组。
• 不断对IV 加密 ,加密,加密。

计数器模式 （CTR）

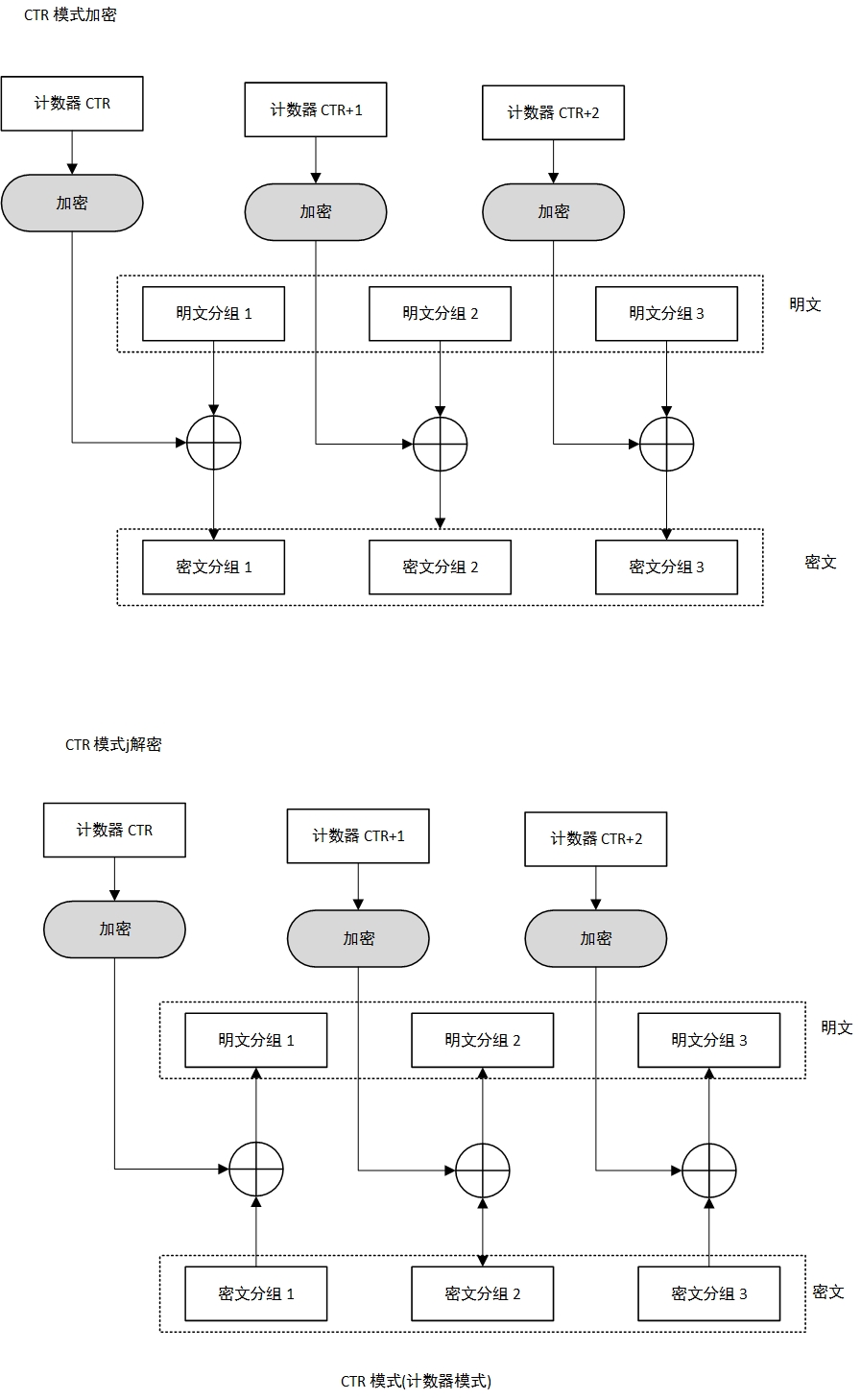
• 计数器每次+1再加密与当前分组XOR得到当前分组密文。

公钥密码

密钥配送问题

使用对称密码，A 加密数据后发送给B , B 需要相同的密钥才能解密，这样A需要把密钥发送给B ,这个过程密钥被截获就可以解密所有数据。

密钥配送问题：对称密码的密钥需要被发送，但又不能直接被发送。

解决方式：

1. 通过事先共享密钥解决。
2. 通过密钥分配中心解决。
3. 通过 Diffie-Hellman 密钥交换来解决。
4. 通过公钥密码来解决。

RSA 加密与解密

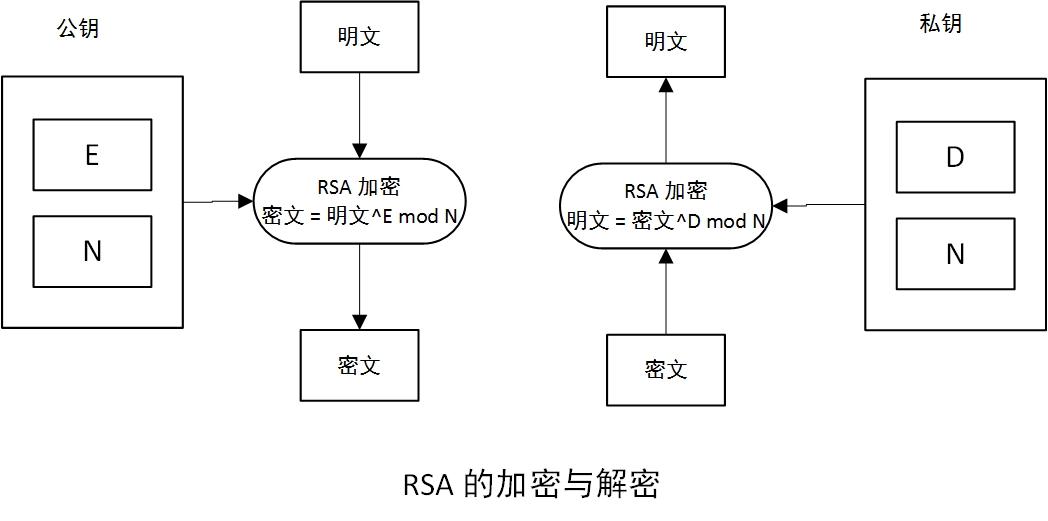
RSA 利用了大整数分解质因数问题的困难度保证机密性。公钥密码一般都是利用数学上的困难问题。

RSA生成密钥对

公钥： N ，E

私钥： N ，D

求公私钥的公共部分 N

$N = p * q（p、q 为大质数）$

求中间数 L

$L = lcm (p-1) * (q-1)$

$(L 是 p-1 和 q-1的最小公倍数)$

求公钥中的 E

$1<E<L$

$gcd(E, L) = 1$

• 求最大公约数可以使用辗转相除法，候选E的生成可以使用伪随机数生成器。
• 求最大公约数可以使用辗转相除法。

求私钥中的 D

$1 < D < L$

$(E * D) mod L =1$

• 其中 (E*D)mod L = 1保证了对密文解密时可以得到原来的明文。

混合密码系统

• 对称加密存在密钥配送问题。

• 公钥加密耗费资源。

• 对称密码 + 公钥密码 + 随机数生成器 -----组合称混合密码系统，集成了对称密码消耗小，公钥密码解决密钥配送的优势。